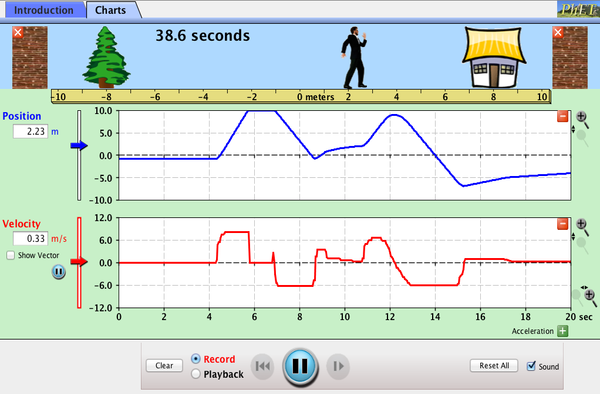
⚿1: Quantities: Δt, Δs, v, a
- Δt : changes in time (not absolute time)
- Δs : changes in position (not absolute position)
- v : velocity
- a : acceleration
⚿2: Relationships: Derivatives & Integrals
| $$ \mathbf { \vec v }(t) = {{ d \, \mathbf {\vec s} (t) } \over { d \, t}} $$ |
$$ \mathbf { \vec a }(t) = {{ d \, \mathbf {\vec v} (t) } \over { d \, t}} $$ |
| $$ \mathbf { \vec v }(t) = \int { \mathbf { \vec a }(t) \, dt } $$ |
$$ \mathbf { \vec s }(t) = \int { \mathbf { \vec v }(t) \, dt } $$ |
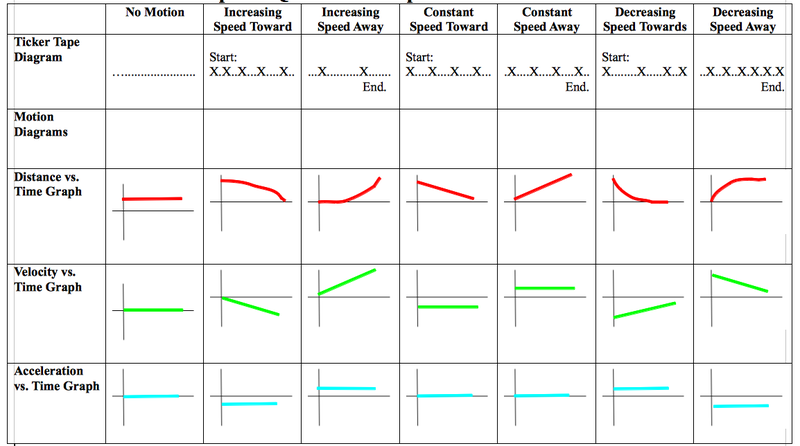
⚿3: Representations: Motion Diagrams & Graphs
Observer at position 0. Draw the motion diagram for each case with vector for v and a. Note all images are for special case of constant acceleration.
Knight Chapter 2 Lecture Slides