Fields: Electric & Magnetic
| Point
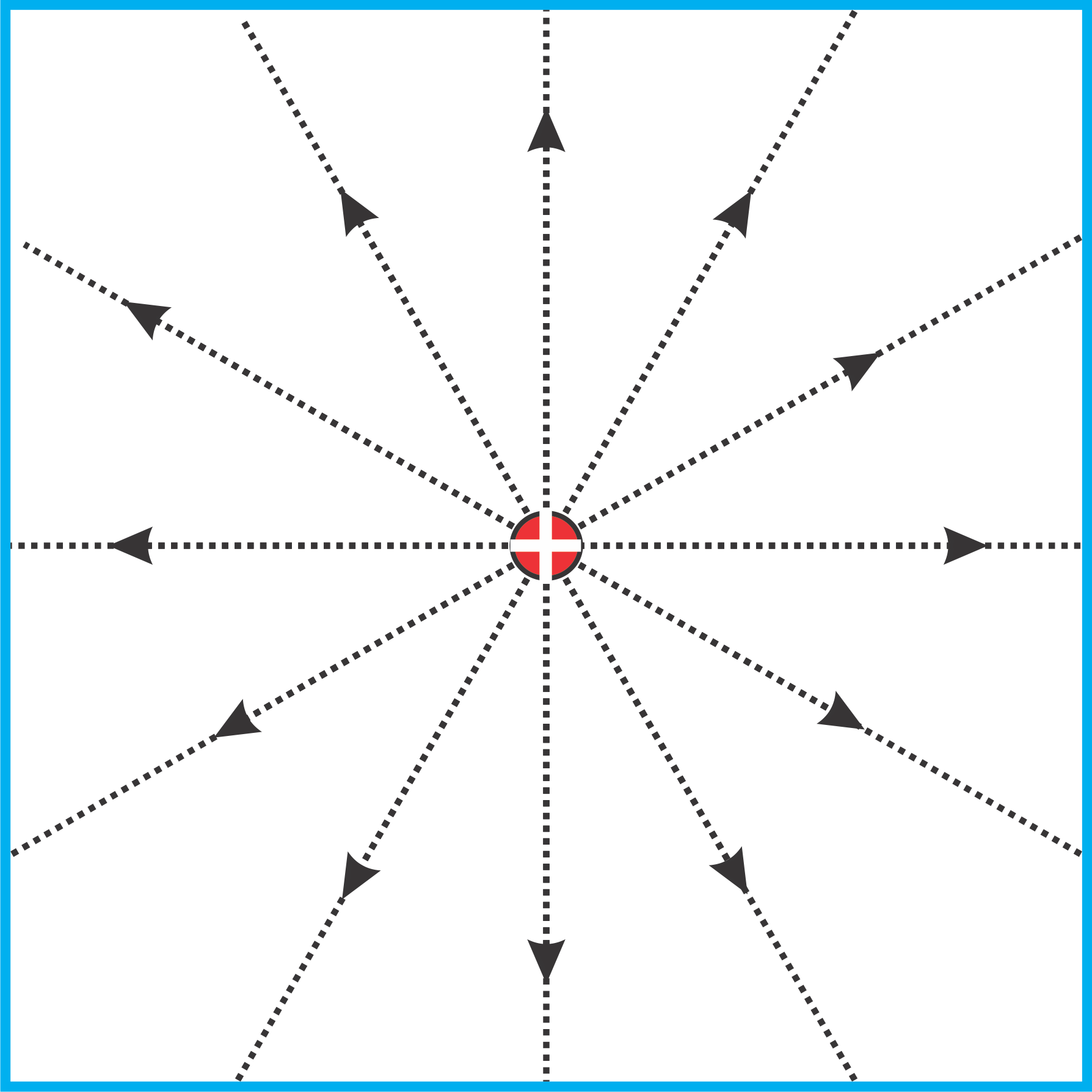
| $$ \mathbf { \vec E }_{point} = {1 \over {4 \pi \epsilon_o}} \, \color{fuchsia} {q \over r^2} \, \mathbf {\hat r } $$
| $$ \mathbf { \vec B }_{point} = {\mu_o \over {4 \pi}} \, \color{fuchsia} {q \over r^2} \, \mathbf {\color{fuchsia} {\vec v}} \times \mathbf {\hat r } $$
|
|---|
|
| Moment
| $$ \mathbf {\vec p} = q \, \mathbf {\vec s} $$
| $$ \mathbf {\vec \mu} = I \, \mathbf {\vec A} $$
|
|---|
| Dipoles (Farfield)
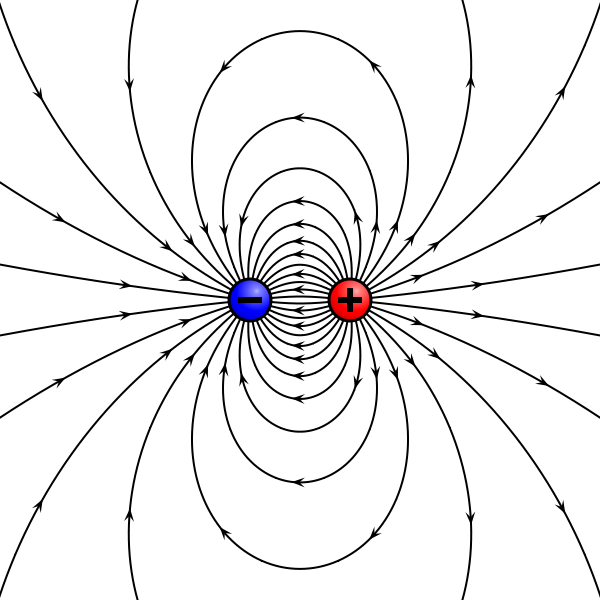
| $$ \mathbf{ \vec E}_{on \,axis} = {1 \over {4 \pi \epsilon_o}} \, \color{fuchsia} {2 \mathbf {\vec p} \over z^3} \mathbf {\hat z} $$
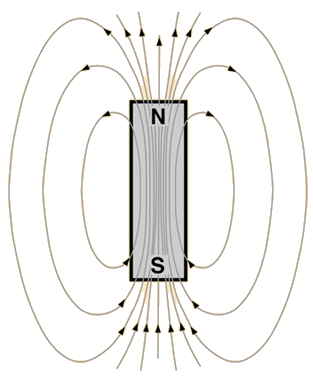
| $$ \mathbf{ \vec B}_{on \,axis} = {\mu_o \over {4 \pi}} \, \color{fuchsia} {2 \mathbf {\vec \mu} \over z^3} \mathbf {\hat z}$$
|
|---|
|
| $$ \lambda \, [C m^{-1}] $$
| $$ I \, [C s^{-1} = A] $$
|
|---|
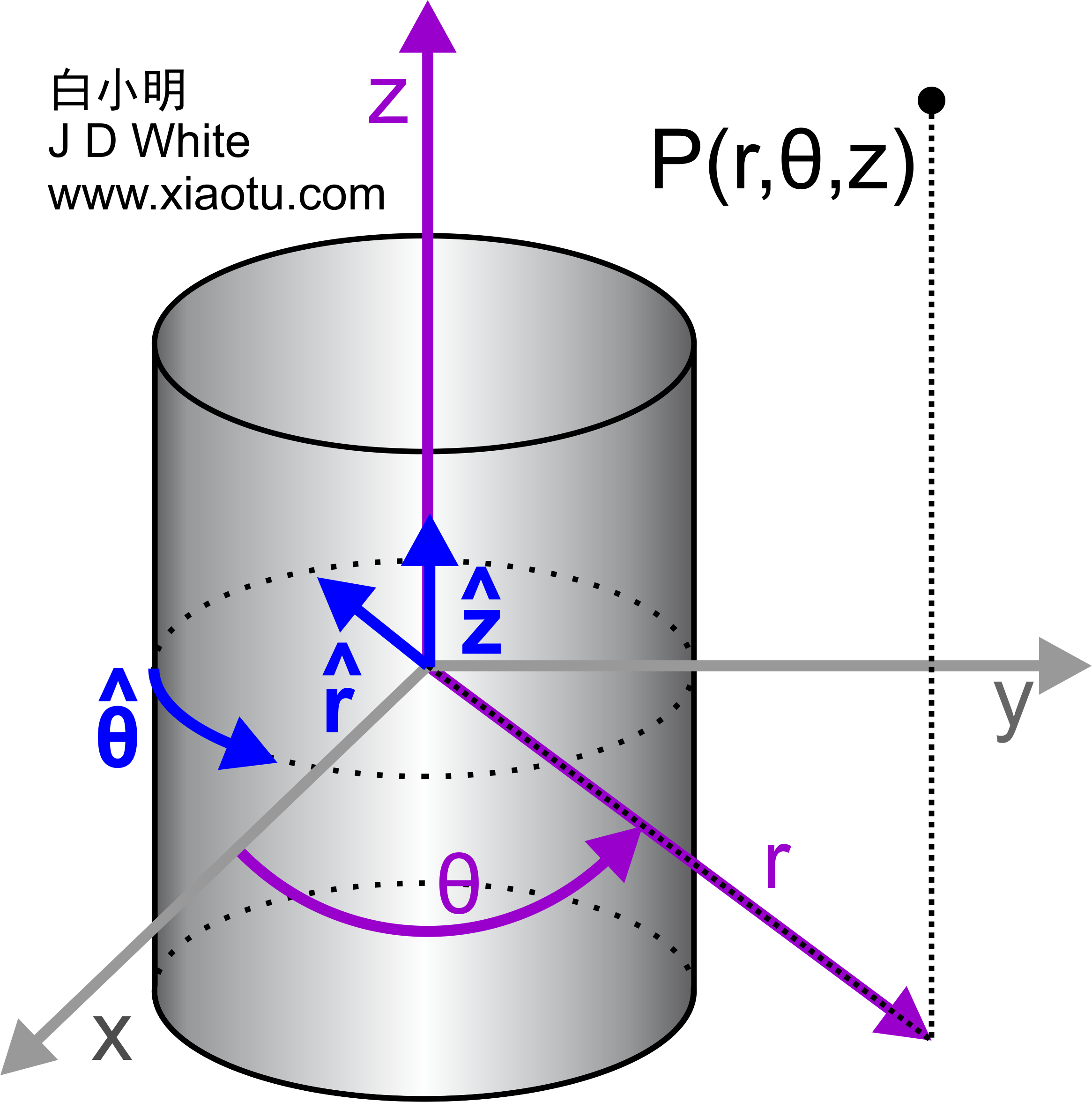
| $$ \mathbf {\vec E}_{line,\infty} = {1 \over {4 \pi \epsilon_o}} \, \color{fuchsia}{2 \lambda \over r} \, { \mathbf {\hat r }} $$
| $$ \mathbf {\vec B}_{wire,\infty} = {\mu_o \over {4 \pi}} \, \color{fuchsia}{2 I \over r} \, { \mathbf {\hat \theta }} $$
|
|
| Gauss & Ampere
| $$ \iint \mathbf {\vec E} \, \cdot d \mathbf {\vec A} = {Q \over \epsilon} $$
| $$ \oint \mathbf {\vec B} \, \cdot \, d \, \mathbf {\vec s} = {\mu_o I} $$
|
|---|
|
| Lorentz | $$ \mathbf a = { m_g \over m_e} \mathbf {\vec G}
+ { q \over m_e} \mathbf {\vec E}
+ { q \over m_e} \mathbf {\vec v} \times \mathbf {\vec B}
$$
|
|---|
| Work | YES! | NO!
|
|---|