Problem Statement
The old man has landed on the top of the roof of my house in Canada. Due to the large amount of ice on the roof, he starts to slide down the roof. Determine the speed at which Santa Claus hits the ground using kinematic equations.
Solution Steps:
- Analyze: Words to labelled Picture
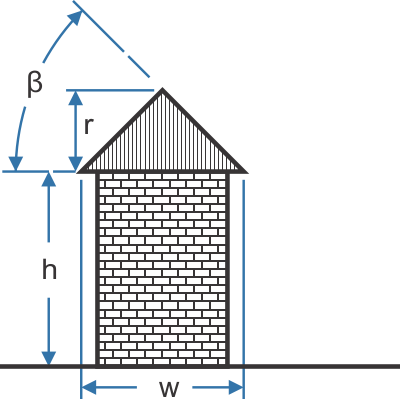
- A Sketch the situation, (What need to find?)
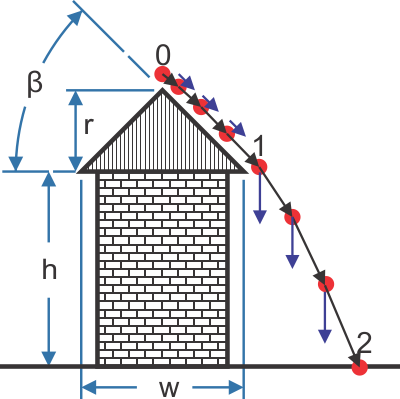
- B Add Motion Diagram (to identify key points in motion)
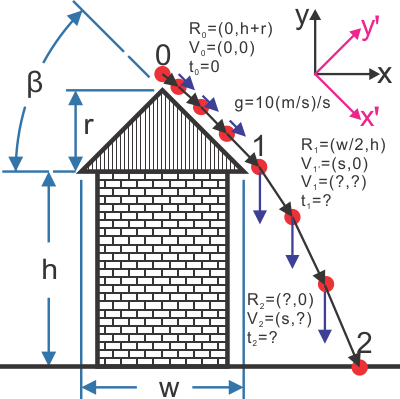
- C Decide on Coordinate System (label key points with know info)
- D Note unknowns
- E Identify the System (Environment)
- What information is missing? Get it.
- Sketch graphs of position, speed and acceleration vs time (Kinematics)
- If forces involved (Dynamics), draw FBD (Free Body Diagrams)
- Think: Divide and Conquer?
- Solve: Bring on the Math (Show steps clearly, units, Significant Figures)
- Assess/Comment/Reflect (Can I solve using Energy ideas?)
1. Analyze: Sketch, Motion Diagram, Coordinate Systems
Require: Speed of Santa at impact on ground.
System: SANTA, Environment: ROOF, EARTH
2. Search To Get Needed Information
h= 6 m, w=5 m, r=2.5, β= π/4, u=0.5 m (distance between houses).
3.Sketch Graphs of motion
4.Draw FBD on roof and in free-fall
5. Think
- Divide and Conquer: Divide into 2 parts : On Roof & Free-fall.
- Coordinate Systems
- On Roof: Choose so motion is 1D (y component is zero)
- Free-fall: Choose so no forces in x-direction of movement.
- Acceleration is constant in each part -- but different values
- We don't care about time (it is not asked about) -- only impact speed so we can use energy methodology to check our answer.
6. Bring in the Math
A: On the Roof: vy'(t)=0, ay'(t)=0, Solve for v1,x' knowing vx'(0)=0
$$ a_{x'} = g \, \sin (\beta) \qquad (1)$$
$$ v_{x'}(t) = a_{x'} \Delta t \qquad (2, since \, a \, is \, constant)$$
$$ \Delta s_{x'}(t) = { a_{x'} \over 2 } \Delta t^2 \, \rightarrow \,
\color{blue}{\Delta t} = \sqrt { 2 \Delta s_{x'}(t) \over a_{x'} }
\qquad \text {(3, integrate 2)} $$
$$ v_{x'}(t) = \sqrt { 2\, a_{x'} \, \Delta s_{x'}(t) } \qquad \text {(4, sub 3 into 2)} $$
$$ v_{1,x'} = \sqrt {2\, a_{x'} \, ( s_{1,x'} - s_{0,x'} )}
= \sqrt {2 \, g \, \sin (\beta) \sqrt {r^2 + (w/2)^2 } } \approx 6 {m \over s}$$
B: Rotate Velocity into vertical-horizontal coordinate system (θ = β = π/4)
$$ \vec {v_1} = (6 \cos (\beta), -6 \sin (\beta)) = (4.4, -4.4) {m \over s}$$
C: Free Fall Portion of Motion: Calculate Impact Velocity
$$ v_{2,x} = 4.4 {m \over s} \, $$
$$ v_{2,y} = - \sqrt {2\, a_y \, (s_{2,y}\, - \, s_{1,y}) + v_{1,y}^2 }$$
$$ v_{2,y} = - \sqrt { 2 \times 10 \times 6 + 4.4^2 }\approx -12 {m \over s} $$
$$ \vec v_{2} = (4.4,-12) \; {m \over s} = (15,-43) \; {km \over hr} \,$$
Ouch!
8. Assess and Comment
- Ouch,
- Seems reasonable. People die when they fall off roofs in Canada.
- Comment: Note number of significant figures in final answer
9. Alternate Solution Method Available
Check using Energy Principle (System = Santa, Environment: Roof, Earth)
$$ \Delta E_{sys} = W $$
$$ {1 \over 2} m v_2^2 - {1 \over 2} m v_0^2 = m g \, ( h + r) $$
$$ {1 \over 2} m v_2^2 = m g ( h + r) $$
$$ |v_2| = \sqrt {2g ( h + r)} = \sqrt { 2 \times 10 \times (6+2.5) }
= 13 \; [m/s] $$
Check using Law of Energy Conservation (System = Earth & Santa & Roof)
$$ \Delta E_{sys} = 0 $$
$$ {1 \over 2} m v_0^2 + m g (h+r)= {1 \over 2} m v_2^2 + 0 $$
$$ |v_2| = \sqrt {2g ( h + r)} = \sqrt { 2 \times 10 \times (6+2.5) }
= 13 \; [m/s] $$